“常见几何体外接球半径求法”的3种“高效”途径

福建省泉州第一中学   数学组  胡积谋13599222132

 

摘要：常见几何体外接球的半径的求法是高考中的一个高频考点，学生从对几何体的观察、探究、到总结形成一般性的解法，有助于学生认识几何体外接球半径求法的本质，同时也让学生学会“转化”,在空间转化中提高逻辑思维能力.

 

关键词   外接球      半径    补形法    “汤勺”形     “图钉”形

几何体外接球的相关考查历来是高考的一大热点与难点，而求解球的体积与面积本质上是球半径的求解问题。在高考中,在关于几何体外接球的半径求解时，如何寻找一种高效的途径，以利考生总结归纳，并高效作答，是我们所应注重的教学内容之一。本文从历年高考有关于外接球半径考查中，总结了“常见几何体外接球半径求法”的3种“高效”途径，与大家一起共勉。

途径1：补形法

长方体的外接球知识点是教科书中学生接触几何体外接球概念的最初的几何体范例，通过学习我们知道外接球的球心与长方体的中心重合，长方体的体对角线过球心，长方体的体对角线的长度就是球的直径，如图，

 

 

 

在这个基础上,若是一些具有长方体局部特征的几何体，如以下三种几何体，

 

 

 

棱柱   三棱锥    三棱锥

 

 

 

 

 

就可以通过补形法将几何体补体还原为长方体，

利用上述长方体与外接球的内在关系，

快速求得外接球的半径：

途径2：“汤勺”形几何体外接球半径的求法

注：“汤勺”形几何体指有一条侧棱（或母线）垂直底面的几何体

具有“汤勺”形特征的几何体（棱锥、棱柱及圆柱）存在外接球时，

如下列几何体，

 

                                      

三棱锥                 四棱锥                          

 

棱柱         

 

 

由特征图形中的线段关系得到共同的特征式：，进而求得球的半径.

 

途径3：“图钉”形几何体外接球半径的求法

注：“图钉”形几何体指椎体顶点在底面的射影为底面

外接圆的圆心的几何体.

 

 

 

具有“图钉”形特征的几何体（棱锥或圆锥）存在外接球时，

如下列几何体正三棱锥与正四棱锥，

 

                                                        

 

 

 

 

 

 

由特征图形中的线段关系得到共同的特征式：，进而求得球的半径.

总结：当然球内接几何体的形状有很多类型，方法与途径并没有固定化的途径，但在高考中常见几何体外接球的半径求法，一般以使用上面三种途径求外接球半径的方法最为常见，在历次考察中出现频率最多，掌握了以上三种途径一般就可以高效的求解几何体外接球的半径，

(1)   补形法根据几何体具有局部的长方体特征，可以很快的寻找到补形的思路，利用长方体的题对角线与球直径的关系，迅速得到答案；

(2)   在求“汤勺”形与“图钉”形几何体的外接球半径的过程中，我们只需要根据几何体特征去确定这类型几何体中的与，结合图形特征所对应的代数方程关系列式求外接球的半径；

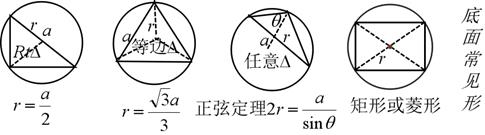
(3)   底面多边形的外接圆的半径，一般的求法根据其底面多边形的特征常见的有以下几个类型：

 

       

 

参考文献：薛胜菊  《揭开多面体外接球的面纱探析多面体外接球半径求法》 《数理化题研究》2014年（9期）