用“数轴穿根法”解不等式

              ——再议“一元二次不等式的解法”

数学组 黄泽兰

一、现状分析

从教二十多年，职业中专的学生的数学基础越来越差。“一元二次不等式的解法”更是学生普遍遇到的难题。多年来教材的教授的方法一变再变，从一开始的与初中一脉相承的“分解——化组——求组解——定原解”，到现在的利用二次函数的图像求解。前者运算繁琐，学生缺乏耐心和必备的运算能力，后者数形结合，学生的思维能力差，常常出现以下问题：

生搬硬套口诀“大于取两边，小于取中间”，而没有注意到根的大小，例如把误解为

对于方程的△<0的情况，学生很难掌握，除了个别成绩好的学生能理解，其他的学生全靠死记硬背，或者干脆放弃不学。例如，方程没有实数根，但为什么不等式的解集是R？

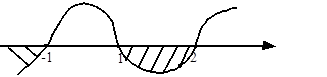我也曾经为此做出不同的探讨，写过一篇“利用二次函数的图像求解”的教学反思。但是面对越来越差的学生，我又产生新的困惑，有没有一种通用的方法，让学生容易理解呢？本学期新接手一个幼教班，我尝试着用“数轴穿根法”讲授。形象直观，课后反馈学习效果很好。

二、“数轴穿根法”的用法

第一步：达标——通过不等式的诸多性质对不等式进行移项，使得右侧为0，并保证x最高次项系数为正！

例如：将-x2-x+2<0化为x2+x-2>0，再化成(x-2)(x+1)>0

第二步：求零点——将不等号换成等号解出所有根。

例如：(x-2)(x+1)=0的根为：x1=2，x2=-1

第三步：在数轴上从左到右依次标出各根（零点）。

例如：-1 , 2

第四步：画穿根线：以数轴为标准，从“最右根”的右上方穿过根，往左下画线，然后又穿过“次右根”上去，一上一下依次穿过各根。

第五步：观察不等号，如果不等号为“>”，则取数轴上方，穿跟线以内的范围；如果不等号为“<”，则取数轴下方，穿跟线以内的范围。

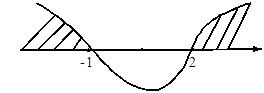例如：若求(x-2)(x+1)>0的解。

在数轴上标根得：-1, 2

画穿根线：由右上方开始穿根。

因为不等号为“>”则取数轴上方，穿跟线以内的范围。即：x<-1或x>2。

对于高次不等式也一样。如，(x-2)(x+1)(x-1)<0，

在数轴上标根得：-1,1， 2

 

不等式的解是：x<-1或1<x<2。

三、穿根法的奇过偶不过定律

就是当不等式中含有单独的x偶幂项时，如，穿根线是不穿过零点x=1的。但是对于X奇数幂项，如，就要穿过零点x=1了。也是奇过偶不过。可以简单记为“奇穿过，偶弹回”。

例如 ：

 有1个零点,X=1

先画一根数轴（X轴），描这个点，再从右向左，从上向下

画线，指数是2为偶，就不穿直接弹回。画成下图：

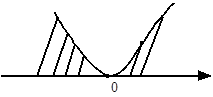
故的解是；而的解包括了零点，故它的解是；解集是空集。

再如，有2个零点X=0，X=1。在x=1出不穿直接弹回，如图。故，

四、无零点的不等式的画线原则

对于无零点的不等式，则无根可穿，就在x轴的上方画线，无论怎样变化，快接近x轴就弹回，不与x轴相交，结论同“第五步”。

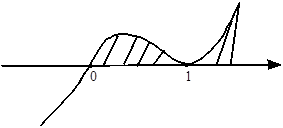例如，无零点。不等号为“>”，则取数轴上方，穿跟线以内的范围，故其解集是R。的不等号为“<”，则取数轴下方，穿跟线以内的范围，故其解集是空集。

综上述，解不等式的关键就是达标，然后求零点！然后运用“穿根法”可以直观地得出答案，而且举一反三，一通百通，同样适用于高次不等式。

一点说明

在教学的过程中，要先让学生熟悉用“穿根法”解二次不等式的方法、步骤后，才提出此法也适用于高次不等式，使学生进一步掌握“穿根法”，才不会使他们觉得负担。